If two dice are rolled one time, find the probability of getting these results.
i. A sum of 2 or 9.
To find the probability of obtaining a sum of 2 or 9. We list the possible sums of 2 and 9.
The combinations that could result in a sum of 2 or 9 is;
Now we can compute the probability;
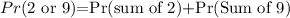
Next, we can get those probabilities;
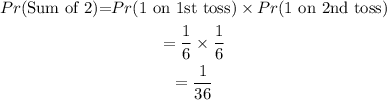
and;
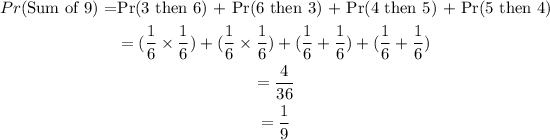
Then the total probability becomes;
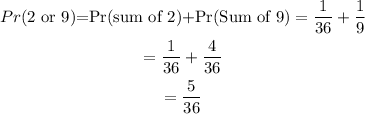
Therefore, If two dice are rolled one time, find the probability of getting a sum of 2 or 9 is 5/36