We are given the time for an object to complete 20 revolutions in a circular path. To determine the velocity of the object we need to use the following formula:
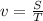
Where:
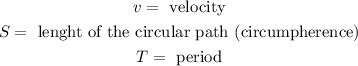
To determine the value of "S" we use the following:
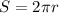
Where:
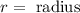
Now, we substitute in the formula for the velocity:
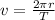
To determine the period we need to divide the time to complete the 20 revolutions by the number of revolutions, like this:
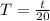
For example, let's take the first value and plug it into the formula:
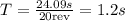
Now, we plug in the value of the radius and the period in the formula for the speed and we get:
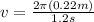
Solving the operations:
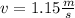
Therefore, the velocity of the bob is 1.15 m/s.