Question

Hi , can you help me to solve this exercise, please!

Answer 1

We can solve this problem by means of the reference angle approach, which consistes in locate the reference angle (the one that makes the arms of the given angle with the x-axis), construct the right triangle and apply the definitions of the trigonometric functions. Then, lets draw a picture of our problem:

Then, the trigonometric function value of angle theta will be the same as the trigonometric value of the reference angle alpha, for instance,

`\csc \theta=\frac{\sqrt[]{143}}{-11}=-\frac{\sqrt[]{143}}{11}`

Then, by applying the definition of the cotangent function:

`\cot \alpha\text{ =}\frac{\text{side adjacent to }\alpha}{side\text{ opposite to }\alpha}`

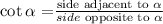
we have that

`\cot \theta=\frac{\sqrt[]{22}}{-11}`

We can simplify this result as follows

`\cot \theta=\frac{\sqrt[]{22}}{-11}=-\frac{\sqrt[]{2*11}}{11}=-\frac{\sqrt[]{2}}{\sqrt[]{11}}`

Therefore, the answer is:

`\cot \theta=-\frac{\sqrt[]{2}}{\sqrt[]{11}}`