Question

In a group of 300 students, 180 students take Math, 210 take English, and 145 take both. a) If we randomly select a student, what is the probability that the student takes Math or English, but not both? b) If we randomly select a student, what is the probability that the student takes neither English nor Math?

Answer 1

From the question;

The group consist of 300 students

therefore

`n(\xi)\text{ = 300}`

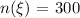
180 students take Math, 210 take English, and 145 take both

Let

Mathematics = M

English = E

Then

`\begin{gathered} n(M)\text{ = 180} \\ n(E)\text{ = 210} \\ n(M\cap E)\text{ = 145} \end{gathered}`

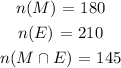
Representing the information on a venn diagram

From the venn diagram

x represent number of pupils taking maths only

Therefore

`\begin{gathered} x\text{ = n(M) -n(M }\cap\text{ E)} \\ x\text{ = 180 - 145} \\ x\text{ = 35} \end{gathered}`

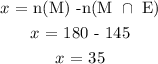
y represents the number of pupils taking english only

Therefore,

`\begin{gathered} y\text{ = n(E})\text{ - n(M }\cap E) \\ y\text{ = 210 - 145} \\ y\text{ = 65} \end{gathered}`

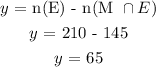
z represents the number of students taking non of the subjects

Therefore

`\begin{gathered} z\text{ = n(}\xi)\text{ - \lbrack n(M only) + n(M }\cap E)\text{ + n(E only) \rbrack} \\ z\text{ = 300 - \lbrack 35 + 145 + 65\rbrack} \\ z\text{ = 300 - 245} \\ z\text{ = 55} \end{gathered}`

a. If we randomly select a student, what is the probability that the student takes Math or English, but not both?

`\begin{gathered} P(\text{ maths or english but not both)} \\ =\text{ P( Maths only) + P( English only)} \\ =\text{ }\frac{n(\text{maths only)}}{\text{total students}}\text{ + }\frac{n(\text{english only)}}{total\text{ students}} \\ =\text{ }(35)/(300)\text{ + }(65)/(300) \\ =\text{ }\frac{35\text{ + 65}}{300} \\ =\text{ }(100)/(300) \\ =\text{ }(1)/(3) \end{gathered}`

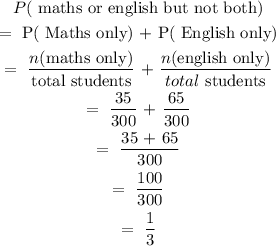
Therefore, the probability that the student takes Math or English, but not both is 1/3

b. If we randomly select a student, what is the probability that the student takes neither English nor Math?

`\begin{gathered} P(neither\text{ maths nor english)} \\ =\text{ }\frac{no.\text{ of students taking non of the subjects}}{\text{Total students}} \\ =\text{ }(55)/(300) \\ =\text{ }(11)/(60) \end{gathered}`

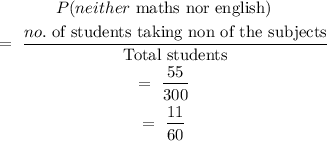
Therefore, the probability that the student takes neither English nor Math

is 11/60