For solving the problem we have to notice the following:
With this information we can predict the form of the figures n=4 and n=15
For each step, there will be
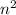
small squares, where n is number of the step. So for step 4 there are 16 small squares and for n=15 there will be 225 small squares.
Finally the equation that represents the relation between the number of step and the number of small squares is
