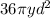Question

Find the area of the shaded sector of the circle. Leave your answer in terms of
`\pi`

Answer 1

The area of a circular sector is proportional to the central angle that it encloses.

Since the non-shaded region encloses an angle of 200°, then the shaded region must enclose an angle of 160°, so that 200+160=360.

Multiply the area of a complete circle by 160/360 to find the area of the shaded sector.

The area of a circle is given by:

`A=\pi r^2`

Then, the area of a circular sector that encloses an angle k measured in degrees, is:

`A=\pi r^2\cdot(k)/(360)`

In the given diagram, we can see that the radius equals 9yd. Then, the area of the shaded sector is:

`\begin{gathered} A=\pi(9yd)^2\cdot(160)/(360) \\ =\pi\cdot81\cdot(4)/(9)yd^2 \\ =36\pi yd^2 \end{gathered}`

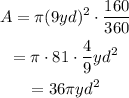
Therefore, the area of the shaded sector is:

`36\pi yd^2`