Question

How many gallons were consumed by each of the two cars that week?

Answer 1

Assume that the first car used x gallons, and the second car used y gallons this week

Since the total number of gallons is 60, then

`x+y=60\rightarrow(1)`

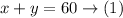
Since the rate of the first car is 40 miles per gallon

Since the rate of the second car is 20 miles per gallon

Then the first car made (40)(x) miles, and the second car made (20)(y) miles

Since the total distance they made is 1900 miles, then

`40x+20y=1900\rightarrow(2)`

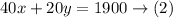
Now, we have a system of equations to solve it.

Multiply equation (1) by -20 to make the coefficients of y equal and different in signs to eliminate it

`\begin{gathered} (-20)(x)+(-20)(y)=(-20)(60) \\ -20x-20y=-1200\rightarrow(3) \end{gathered}`

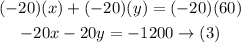
Add equations (2) and (3)

`\begin{gathered} (40x-20x)+(20y-20y)=(1900-1200) \\ 20x+0=700 \\ 20x=700 \end{gathered}`

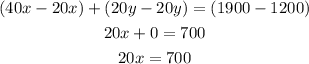
Divide both sides by 20

`\begin{gathered} (20x)/(20)=(700)/(20) \\ x=35 \end{gathered}`

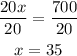
Substitute the value of x in equation (1) to find y

`35+y=60`

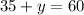
Subtract 35 from both sides

`\begin{gathered} 35-35+y=60-35 \\ y=25 \end{gathered}`

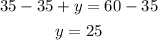
The first car used 35 gallons

The second car used 25 gallons