Question

Suppose Halley's comet orbits the Sun every 67 years and has an eccentricity of 0.97. What is the perihelion distance of Halley's comet in AU?

Answer 1

We are asked to determine the perihelion distance of Halley's comet. To do that we will use the following formula:

`P=a(1-e)`

Where:

`\begin{gathered} P=\text{ perihelion distance} \\ a=\text{ distance of semi-major ax}is \\ e=\text{ excentricity} \end{gathered}`

To determine the distance of the semi-major axis we will use Kepler's third law

`T^2=a^3`

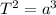
Where:

`\begin{gathered} T=\text{ period in earth years } \\ a=\text{ distance of semi-major ax}is\text{ in Astronomical Units. } \end{gathered}`

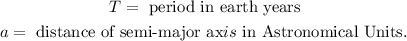
Now, we solve for "a" by taking the cubic root on both sides:

`\sqrt[3]{T^2}=a`

Now, we substitute the value of "T":

`\sqrt[3]{(67years)^2}=a`

Solving the operations:

`16.5AU=a`

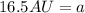
Now we substitute this value in the formula for the perihelion:

`P=(16.5AU)(1-0.97)`

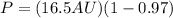
Solving the operations:

`P=0.5AU`

Therefore, the perihelion distance is 0.5 Astronomical Units.