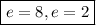Answer:
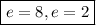
Explanation:
1. Expand
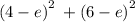
Expand each term in the expression using the identity
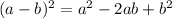
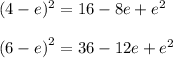

Combining like terms we get

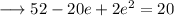
Subtract 52 from both sides and rearrange terms:

Divide both sides by 2
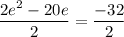
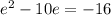
To rewrite in the form (x+a)² = b
we must have 2ae = -10e and therefore a = -5
So the expression
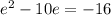
can be transformed by
Adding (-5)² to both sides to complete the square:
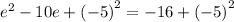
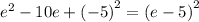
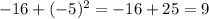 \
\
So we get
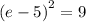
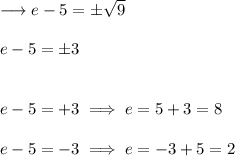
So the solution set is