We have the following set of equations,
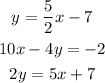
To know whether they are parallel or perpendicular we need to have all three equations in slope-intercept form, or

Line 1,
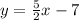
Line 2,
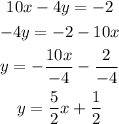
Line 3,
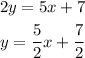
Notice, all three lines have a slope of m = 5/2
Since the slopes are all the same, all three lines are parallel