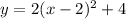Given:
Vertex ===> (h, k) (2, 4)
The parabola passes through the point: (x, y) ==> (3, 6)
Let's find the equation of a parabola.
To find the equation, use the general equation of a parabola with vertex (h, k):
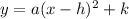
Where:
(h, k) ==> (2, 4)
(x, y) ==> (3, 6)
Substitute values into the general equation:
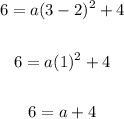
Subtract 4 from both sides:
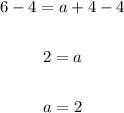
Substitute 2 for a, and input the values of the vertex (h, k) in the general vertex equation:
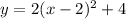
Therefore, the equation of the parabola is:
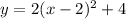
ANSWER: