A) Check the graph, below
B) $518.38 (y=19.771x+300.9)
C) r=0.965
A) Let's plot a scatter plot with a trendline for that table:
b) We need to find out the equation by making use of 2 formulas. The first one to find out the slope, and the second to find out the linear coefficient.
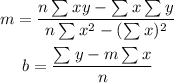
But before that, we need to place in here a table, with the given data:
Considering the last line the summation of each category, we can plug into that formula, and plugging into them the formula we have:
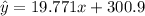
Considering that 2020 would be the 11th year on that table and that we can plug into that equation, for the first one 2009 is the 0th year.
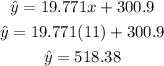
So in 2020, the cost for a family would be $518.38 note that above the prediction base on only two points.
C) Let's find the correlation coefficient using the following formula:
![\begin{gathered} r=\frac{n\sum^{}_{}xy-(\sum^{}_{}x)(\sum^{}_{}y)}{\sqrt[]{\lbrack n(\sum^{}_{}x^2)-(\sum^{}_{}x)^2\rbrack\lbrack n\sum^{}_{}y^2-(\sum^{}_{}y)^2\rbrack}}= \\ \\ r=\frac{5\cdot5601-15\cdot2102}{\sqrt[]{\lbrack5\cdot55-(15)^2\rbrack\cdot\lbrack5\cdot743492-(2102)^2\rbrack}} \\ r=0.965 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5a4cozwsdbfin5aws00fbhxmoh5l3lm4b5.png)
Note that n=5, ∑x=15, ∑xy=5601, ∑y=2102, ∑x²=55, and we've plugged into that and find a positive correlation.