Question

The surface areas of two similar solids are 450 mm? and 578 mm?. If the volume of the smaller solid is 511 mm?, find thevolume of the larger solid. Round your answer to the nearest hundredth.A. 724.12 mm^3B. 733.59 mm^3C. 734.33 mm^3D. 743 86 mm^3

Answer 1

Given:

• Surface area of solid 1 = 450 mm²

,

• Surface area of solid 2 = 578 mm²

,

• Volume of solid 1 = 511 m³

Let's find the volume of the larger solid.

To find the volume of the larger solid, let's find the scale factor since the solids are similar:

We

`\begin{gathered} k^2=\frac{surface\text{ area of solid 2}}{surface\text{ are of solid 1}} \\ \\ k=\sqrt{(578)/(450)} \\ \\ k=√(1.2844) \\ \\ k=1.133 \end{gathered}`

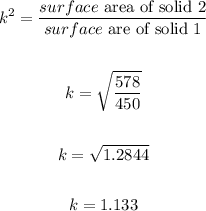
Now, to find the volume of the larger solid we have:

`\begin{gathered} (V_2)/(V_1)=k^3 \\ \\ (V_2)/(511)=1.133^3 \\ \\ V_2=1.133^3*511 \\ \\ V_2=743.86\text{ mm}^(^3) \end{gathered}`

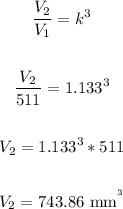
Therefore, the volume of the larger solid is 743.86 mm³.

ANSWER:

D. 743.86 mm³.