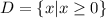Given:
![\begin{gathered} f(x)=\sqrt[]{x} \\ g(x)=4x+7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i615ohvqzee2e88rhycypbkbumk3vnehed.png)
To find:
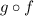
And its domain, follow the steps below.
Step 01: Substitute x in g(x) by f(x).
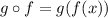
Then, given g(x), substitute x in this equation by f(x).
![\begin{gathered} g(x)=4x+7 \\ g(f(x))=4\cdot\sqrt[]{x}+7 \\ g(f(x))=4\sqrt[]{x}+7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vefxip8f7ea4jmjvpsj9i0j3kqlnv7zgqm.png)
Thus,
![g\circ f=g(f(x))=4\sqrt[]{x}+7](https://img.qammunity.org/2023/formulas/mathematics/college/ovbbcht813dqjgzyl734dhsqqqm5c1bpus.png)
Step 02: Find the domain.
The domain is the set of all possible input values, that is, the set of all possible x-values.
Since there is no square root of negative roots, x can not be negative.
Then, the domain is x ≥ 0.
Domain:
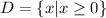
Answer:
gof:
![g\circ f=4\sqrt[]{x}+7](https://img.qammunity.org/2023/formulas/mathematics/college/hmmzg5ti8kd7yqah869cf8f7qidservy93.png)
Domain: