Question

The points L(0,−8)(0,−8), M(5,−8)(5,−8), N(9,0)(9,0), and O(4,0)(4,0) form parallelogram LMNO. Plot the points then click the "Graph Quadrilateral" button. Then find the perimeter of the parallelogram. Round your answer to the nearest tenth if necessary.

Answer 1

The points are provided in the question to be:

`\begin{gathered} L=(0,-8) \\ M=(5,-8) \\ N=(9,0) \\ O=(4,0) \end{gathered}`

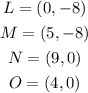
The parallelogram is drawn below:

By the definition of a parallelogram, the opposite sides have the same lengths. Therefore:

`\begin{gathered} LO=MN \\ ON=LM \end{gathered}`

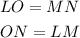
Recall the distance formula:

`d = √((x_2 - x_1)^2 + (y_2-y_1)^2)`

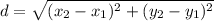
Applying the formula to the lines of the parallelogram, the lengths are:

`\begin{gathered} LO=MN=8.94 \\ ON=LM=5 \end{gathered}`

Therefore, the perimeter of the shape will be:

`Perimeter=2(8.94+5)=27.88`

The perimeter is approximately 27.9 units.