a)
Functions given:

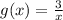
Procedure
• f(g(x))
Substituing g(x) in the x present in f(x)
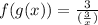
Simplifying:
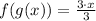

• g(f(x))
Substituing f(x) in the x present in g(x)
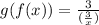
Simplifying
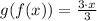
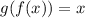
Since f(g(x)) = g(f(x)) = x, the given equation and the computed inverse are really inverse functions.
b)
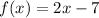

• f(g(x))
Substituing g(x) in the x present in f(x)

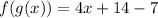
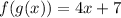
• g(f(x))
Substituing f(x) in the x present in g(x)
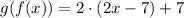

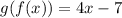
Then, these functions are NOT inverse.
Answer:
• a) ,f and g are inverses of each other
,
• b) f and g are not inverses of each other