Given the System of Equations:

The exercise asks for solving it graphically. Then, in this case, you need to graph both lines in order to determine the solution of the system.
In order to graph it, you can find the x-intercepts and the y-intercepts:
1. It is important to remember the Slope-Intercept Form of the equation of a line:

Where "m" is the slope of the line and "b" is the intercept.
In this case, you can identify that the y-intercept of the first line is:

And the y-intercept of the second line is:
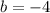
2. By definition, the value of "y" is zero when the line intersects the x-axis.
Then, you need to substitute the following value of "y" into each equation and then solve for "x", in order to find the x-intercept of each line:

- For the first line, you get:
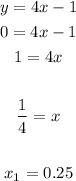
- For the second line, you get:
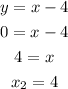
3. Now you know that the first line passes through these two points:
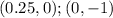
And the second line passes through these two points:

4. Knowing those points, you can graph the lines:
Notice that the line intersect each other at