Question

Given that sin A = -4 over 5 and angle A is in quadrant 3,what is the value of sin (2A)

Answer 1

Case: Trigonometry (Quadrants)

Given:

`\begin{gathered} sinA=\text{ -}(4)/(5) \\ In\text{ quadrant 3} \end{gathered}`

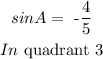
Required:

Find sin (2A)

Method:

Step 1: First we find the acute angle A, that sinA = 4/5

`\begin{gathered} sinA=\frac{\text{ 4}}{5} \\ A=\text{ }\sin^(-1)((4)/(5)) \\ A=\text{ 53.13} \end{gathered}`

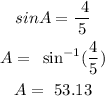
From here,

CosA is:

`\begin{gathered} cosA=\text{ }(adj)/(hyp) \\ using\text{ the 3-4-5 pythagoras rule, adj=3} \\ cosA=\text{ }(3)/(5) \end{gathered}`

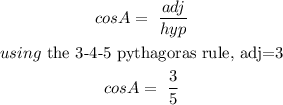
Step 2: Rotate the angle into the 3rd quadrant

A*= 53.13 + 180

A*= 233.13.

Step 3: Sin (2A)

`\begin{gathered} sin(2A)=\text{ 2sinAcosA} \\ sin(2A)=\text{ 2}*\text{\lparen}(-4)/(5)\text{\rparen}*(\frac{\text{-3}}{5}\text{\rparen} \\ sin(2A)=\frac{\text{ 24}}{25} \end{gathered}`

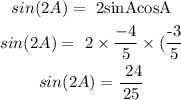
Final answer:

The value of sin(2A)= 24/25