Question

Can you please help me with one of these or both

Answer 1

Given,

The mass of the gymnast, m=40 kg

The initial speed with which the gymnast enters the foam ball pit, u=7 m/s

The average resistive force applied by the foam balls, F=-1000 N

The negative sign indicates that the force is resistive in nature.

From Newton's second law,

`F=ma`

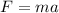
Where a is the acceleration with which the gymnast slows down after entering the pit.

On substituting the known values,

`\begin{gathered} -1000=40* a \\ \Rightarrow a=(1000)/(40) \\ =-25\text{ m/s}^2 \end{gathered}`

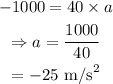
As the foam balls oppose the motion of the gymnast, the gymnast comes to rest after a certain period of time. Thus, the final velocity of the gymnast is v=0 m/s

From the equation of motion,

`v^2-u^2=2ah`

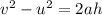
Where h is the depth reached by the gymnast in the pit before coming to rest.

On substituting the known values,

`\begin{gathered} 0-7^2=2*-25* h \\ \Rightarrow h=(-7^2)/(2*-25) \\ =0.98\text{ m} \end{gathered}`

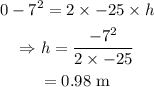
Thus the gymnast reaches a maximum depth of 0.98 m.