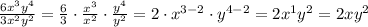We need to define two terms in the form:
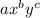
with a, b, and c constants. Then, we need to find the quotient of those terms.
One way to define those terms is by choosing the constants to be, for the first term:
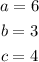
Thus, the first term can be:
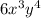
And. for the second term, we could choose, for instance:
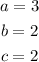
Thus, the second term would be:
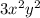
Now, the quotient of those terms can be found by grouping the terms with the same base and applying the rule:
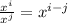
Thus, we obtain: