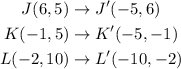Question

Write the coordinates of the vertices after a rotation 90° counterclockwise around the origin.-10-8-6-4-2246810-10-8-6-4-2246810xyJKL

Answer 1

So,

Here we have the following vertices:

`\begin{gathered} L(-2,10) \\ K(-1,5) \\ J(-6,5) \end{gathered}`

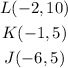
We are going to write the coordinates of the vertices after a rotation 90° counterclockwise around the origin.

Remember that a 90° rotation counterclockwise around the origin follows the rule:

`(x,y)\to(-y,x)`

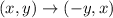
So what we're going to do is to change the x coordinate of all vertices by each coordinate of y with the opposite sign. And, we're going to change the y-coordinate by the x-coordinate. This is,

`\begin{gathered} J(6,5)\to J^(\prime)(-5,6) \\ K(-1,5)\to K^(\prime)(-5,-1) \\ L(-2,10)\to L^(\prime)(-10,-2) \end{gathered}`