ANSWER
6a
Step-by-step explanation
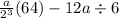
The order of operations is always the same:
0. Parenthesis
,
1. Exponents (include powers and roots)
,
2. Multiplications and divisions
,
3. Additions and subtractions
Let's take a look at the given expression. We have two terms - which are separated by a minus sign. In the first term there's a parenthesis so we have to solve what's inside first. Note that what's inside the parenthesis is just a number, no operation to be done. Therefore for the first step we have:

Now, again in the first term there's an exponent in the denominator. We have no exponents in the second term. Solving 2³ = 8:
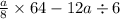
The third operations to solve are multiplications and divisions. We have many of those, but since we have a variable a, it is convenient if we solve the division first in the first term:
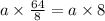
And the division of the second term:
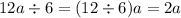
Therefore after solving the third operations we have:
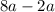
Now we do the subtraction. As mentioned before, there's a variable involved so to solve the subtraction we have to combine like terms. In this case, both terms contain the variable so we take it as common factor:
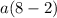
And solve the operation inside the parenthesis:
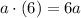
Hence, the expression simplifies to 6a