To determine the inverse function, we will write the function and reach the inversion by performing the required calculation, as follows:
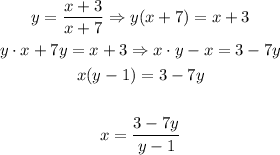
From the solution developed above, we are able to conclude that the solution for the present question is the following:
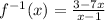
Where the numerator is: 3 - 7x
Ans the denominator is: x - 1