Question

A car traveling at 10.2 meters per second crashes into a barrier and stops at 0.330 meters. What force must be exerted on a child of mass 28..3 kilograms to stop him or her in the same time as the car. Include units in your answer. Answer must be in 3 significant digits.

Answer 1

First, determine the acceleration of the motion of the car, by using the following formula:

`v^2=v^2_0+2ax`

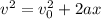
where,

v: final velocity = 0m/s

vo: initial mvelocity = 10.2 m/s

a: acceleration = ?

x: distance = 0.330 m

Solve the equation above for a and replace the previous values of the parameters:

`a=(v^2-v^2_o)/(2x)=((0(m)/(s))^2-(10.2(m)/(s))^2)/(2(0.330m))=-157.636(m)/(s^2)`

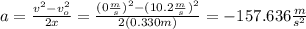
minus sign means that there is a deceleration,

Now, use the Newton second law by using the previous result. Consider that time needed to stop a child with the given mass is the same time obtained with the previous acceleration in case the child moves with the same velocity as the car. Then:

`F=m\cdot a`

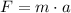
where m = 28.3 kg (mass of the child) and a is the previous result we got. Replace these values to obtain the required force.

`F=(28.3kg)(157.636(m)/(s^2))=4461.109N`

with three significant digits you have:

F = 4461 N