Question

rea84Respond to the following questions:Look at the above figure from section 9.5 in theOpenStax PreAlgebra text. Notice the semicircle onthe left,, and the adjacent right triangle.1. What is the measure of each of the two legs of the righttriangle? How can those measures be used to find themeasure of the hypotenuse?

Answer 1

1. 8,4. With the Pythagorean Relation.

2.a) Find the perimeter of that semicircle and add to that the hypotenuse and the smallest leg.

2b) The Perimeter is approximately 24.6 cm

3a) We would use the semicircle and triangle formula to find the area

3b) The area of that figure is approximately 66.3 cm²

We can find the measure of the missing leg of that triangle by taking the Pythagorean Theorem.

`\begin{gathered} a^2=b^2+c^2 \\ \\ 8^2=4^2+c^2 \\ \\ 4^2+c^2=8^2 \\ \\ 4^2+c^2-4^2=8^2-4^2 \\ \\ c^2=48 \\ \\ c=√(48),\:c=-√(48) \\ \\ c=4√(3),\:-4√(3) \end{gathered}`

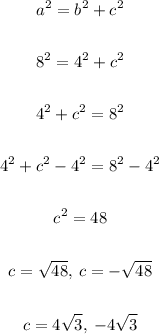
As there are no negative measures, we can tell that leg c is:

`\begin{equation*} c=4√(3), \end{equation*}`

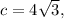
1) So we can answer that by saying that with the help of the Pythagorean Theorem we can find the hypotenuse by considering the diameter of that semicircle as one of those triangle's legs.

2

a) To find the Perimeter of that figure we need to use the semi-circumference measure and then add the hypotenuse and the leg whose measure is 4. This way:

`P=(2\pi r)/(2)+8+4`

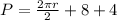
Note that since the diameter is 8, the radius is 4 so let's plug it into that and solve it:

`P=4\pi+12`

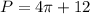
b) We can tell the Perimeter is:

`P=4\pi+12\approx24.6\:cm`

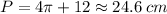
Rounding it off to the nearest tenth.

3) If the point was to find the area, then we'd need to find the area of that semicircle and the area of that triangle.

`\begin{gathered} A=\pu{}\pi r^2+(bh)/(2) \\ \\ A=16\pi+(4*8)/(2) \\ \\ A=16\pi+(32)/(2) \\ \\ A=16\pi+16\approx66.3 \end{gathered}`

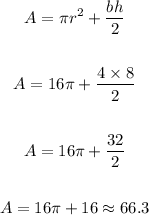
Let's sort the answers out at the top of the page