Question

Which relationship represents a function with the same slope as the function represented above? А

Answer 1

C

Step-by-step explanation

to solve this we need to find the slope of the line in the table,and compare with the options

Step 1

Find the equation of the line

A) find the slope

when you know 2 points of a line, you can find the slope by:

`\begin{gathered} \text{slope}=\frac{change\text{ in y }}{\text{change in x}}=(y_2-y_1)/(x_2-x_1) \\ \text{where P}_1(x_1,y_1)andP2(x_2,y_2) \\ \text{are 2 points of the line} \end{gathered}`

Let

P1(5,28)

P2(9,52)

replace,

`\begin{gathered} \text{slope}=\frac{change\text{ in y }}{\text{change in x}}=(y_2-y_1)/(x_2-x_1) \\ \text{slope}=(52-28)/(9-5)=(24)/(4)=(12)/(2)=6 \\ \end{gathered}`

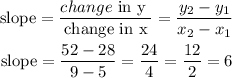
hence, the slope is 6

Step 2

so, the answer is C

I hope this helps you