Step 1. A point P is at a distance of 450m to one end of the pond, and at a distance of 520 m to the other end of the pond. The angle formed between the lines is 115°.
The first step is to make a diagram of the situation:
In red we have the point and the two lines, in green a representation of the point, and the blue line is the length of the pond.
Step 2. A triangle is formed between the red lines and the blue lines. We know two sides and one angle of the triangle, therefore, to solve the problem and find the length of the pond, we use the cosine rule:
Step 3. For reference, we will label the components of our triangle as follows:
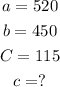
Step 4. Substituting these values into the cosine rule:

Solving the operations:

Solving for c:
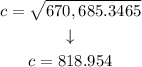
Rounding to the nearest meter:
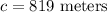
The length of the pond is 819 meters.
Answer:
819 m