Question

Part CImagine two line segments where each represents a slant height of the cone. The segments are on opposite sides of the cone and meet at the apex. Find the measurement of the angle formed between the line segments.Part C is the one I need help with. I don't understand what it wants me to do. The cone to answer the question is in the second image and the question is in the first

Answer 1

Step-by-step explanation:

Part C

The question wants us to get the measurement of the angle formed between the line segments.

We are also told that the line segment is also the slant height

Thus

So we will have to find the angle at C

So, the scope will be to find the half-angle and then multiply by 2

Thus, we will have

Thus, we will have

`tan((\theta)/(2))=(opposiste)/(adjacent)=(2)/(6)=(1)/(3)`

Thus

`\begin{gathered} (\theta)/(2)=\tan^(-1)((1)/(3)) \\ (\theta)/(2)=18.435 \end{gathered}`

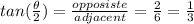
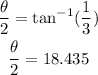
Thus, we will have to get the measurement of the angle as

`2*((\theta)/(2))=2*18.435`

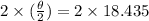
Thus, we have the angle to be 36.87 degrees