We will solve the problem using the substitution method.
The system of equations to be solved is
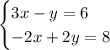
Notice that the second equation is equivalent to
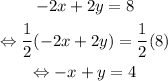
Then,
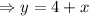
We can substitute the last result into the first equation of the system as shown below
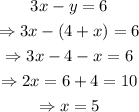
Finally,
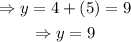
The answer is (x,y)=(5,9)