Question

Please help me find the measure of YW and please leave it in Radical form

Answer 1

Here, we are given the circumcenter of the triagle Y.

THe circumcenter is the point where the three perependicular bisectors of the triangle meet.

Let's solve for the side lengths of SS, SY, YW, YX.

• 4. Given:

ST = 18

Where YV is the perpendicular biscetor, the point V divides The line ST into two equal parts.

Thus, the lenght of SV = VT

`\begin{gathered} SV=(ST)/(2)=(18)/(2)=9 \\ \\ SV=9 \end{gathered}`

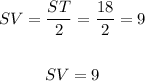
SV = 9 units

• 5. SY

Given:

YT = 14

The length of SY is equal to the length of YT since the vertices are equidistant from the circumcenter.

Thus,

SY = YT = 14

YT = 14 units

• 6. YW

Given:

WU = WT = 11

YT = 14

The triangle TVY forms a right triangle.

To find the length of YW, use pythagorean theorem.

Thus, we have:

`\begin{gathered} YT^2=WT^2+YW^2 \\ \\ YW=\sqrt[]{YT^2-WT^2} \\ \\ YW=\sqrt[]{14^2-11^2} \\ \\ YW=\sqrt[]{196-121} \\ \\ YW=\sqrt[]{75} \end{gathered}`

YW = √75 units

• 7. YX

Given:

SY = 14

SX = 13

The triangle SXY is a right triangle.

To find The lenght of YX use pythagorean theorem

thus, we have:

`\begin{gathered} YX=\sqrt[]{SY^2-SX^2} \\ \\ YX=\sqrt[]{14^2-13^2} \\ \\ YX=\sqrt[]{196-169} \\ \\ YX=\sqrt[]{27} \\ \\ YX=\sqrt[]{27} \end{gathered}`

The length of YX is √27 units

ANSWER:

`\begin{gathered} SV\text{ = 9 } \\ \\ SY\text{ = 14} \\ \\ YW=\sqrt[]{75} \\ \\ YX=\sqrt[]{27} \end{gathered}`