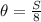The Arc Length
Given a circle of radius r, the arc length, or the distance between two points along the circle that has a central angle of θ, is given by:
S = θ.r
The angle θ must be expressed in radians.
We are given the radius of the Ferris wheel of r=8 m and the distance (arc length) that Kristin travels of S=10.4 meters. We can calculate the central angle in radians solving for θ:
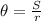
Substituting:
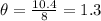
The angle's measure is 1.3 radians.
Now we are required to find the angle when Kristin travels S=24.8 meters.
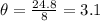
The angle is 3.1 radians.
If we were given different measures of S, the central angle, in radians, can be calculated by the expression: