Question

Jeremiah has $2 worth of dimes and quarters. He has a total of 14 dimes and quarters altogether. Determine the number of dimes, x, and the number of quarters, y, that Jeremiah has.

Answer 1

Jeremiah has 10 dimes and 4 quarters.

Step-by-step explanation:

Let the number of dimes = x

Let the number of quarters= y

Jeremiah has a total of 14 dimes and quarters altogether:

`\implies x+y=14`

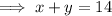
Next:

• 1 dime=$0.10

,

• 1 quarter =$0.25

Jeremiah has $2 worth of dimes and quarters. Therefore:

`0.10x+0.25y=2`

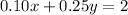
We solve the two equations simultaneously:

`\begin{gathered} x+y=14 \\ 0.10x+0.25y=2 \end{gathered}`

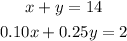
From equation (1):

`x=14-y`

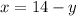
Substitute x=14-y into the second equation:

`\begin{gathered} 0.10(14-y)+0.25y=2 \\ 1.4-0.10y+0.25y=2 \\ 0.15y=2-1.4 \\ 0.15y=0.6 \\ y=(0.6)/(0.15) \\ y=4 \end{gathered}`

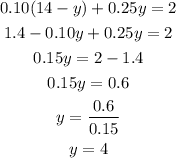
Recall: x=14-y

`\begin{gathered} x=14-4 \\ x=10 \end{gathered}`

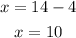
Therefore, Jeremiah has 10 dimes and 4 quarters.

Let the