We have a right triangle with hypotenuse 45 in. long.
We have to find the length of the opposite side to a 60° angle.
We can use the trigonometric ratio:
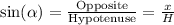
Then, as α = 60° and H = 45 in., we can write:
![\begin{gathered} x=H\cdot\sin (\alpha) \\ x=45\cdot\sin (60\degree) \\ x=45\frac{\sqrt[]{3}}{2} \\ x\approx38.97 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ht1z1kk9efl48tlgk6oecwexeycrct8gce.png)
Answer: the opposite side will have a length of approximate 38.97 inches.