Question

1) What are the values of a and b for each equation? Why does this represent exponential growth? Equation a value b value y= y = – za 2) What will be the y-intercept for each graph? 3) Compare and contrast the value of y as x increases.

Answer 1

Step 1

write out the general formula of an exponential is

`y=ab^x`

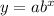
1) Thus for the first equation

`\begin{gathered} y=3^x \\ a=1 \\ b=3 \end{gathered}`

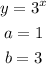
For the second equation

`\begin{gathered} y=-3^x \\ a=-1 \\ b=3 \end{gathered}`

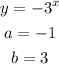
2) For the equation

`\begin{gathered} y=3^x \\ \text{The y-intercept is 1} \end{gathered}`

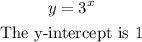
For the equation

`\begin{gathered} y=-3^x \\ \text{the y-intercept is -1} \end{gathered}`

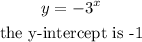
3) For equation

For equation

`y=-3^x`

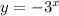
The values of y remain constant for a range of x values and decrease exponentially with further increase of x values