Question

Frederick needs to borrow $3000 for a down payment on a new car. His uncle decided to loan him the money as a 2.5% loan. Frederick doesn't want to pay more than $225 in interest. How many years does Frederick have to pay back the loan?

Answer 1

We are given that Frederick borrows $3000 at an interest rate of 2.5%. We will determine the time for this loan to gain $225. To do that we will use the following formula:

`I=\text{Prt}`

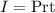
Where:

`\begin{gathered} I=interest \\ P=\text{ principal} \\ r=\text{ interest rate in decimal form} \\ t=\text{ time} \end{gathered}`

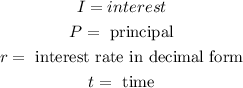
Now we solve for the time by dividing both sides by "Pr":

`(I)/(Pr)=t`

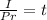
Now, the interest rate in decimal form is determined by dividing the percentage by 100:

`r=(2.5)/(100)=0.025`

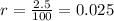
Now we substitute the values:

`(225)/(3000*0.025)=t`

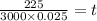
Now we solve the operations:

`3=t`

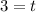
Therefore, the time of the loan must be 3 years.