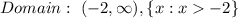Question

Graph the logarithmic function =gxlog4+x2.To do this, plot two points on the graph of the function, and also draw the asymptote. Then, click on the graph-a-function button.Additionally, give the domain and range of the function using interval notation.

Answer 1

Given: A logarithmic function

`g(x)=\log_4(x+2)`

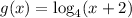
Required: To graph the given function with asymptote and give the domain and range of the function.

Explanation: To graph, the given function draw a table of g(x) and x as follows

Now plotting these points on a graph gives

Now the vertical asymptote can be found by setting argument (x+2) equal to zero.

Which gives x=-2 as an asymptote of the given function.

Now for the domain and range of the function

`Domain:\text{ }(-2,\infty),\lbrace x:x>-2\rbrace`
`Range:(-\infty,\infty),\lbrace y:y\in\Re\rbrace`

Where y=g(x)

Final Answer: Vertical Asymptote occurs at x = -2

`\begin{equation*} Domain:\text{ }(-2,\infty),\lbrace x:x>-2\rbrace \end{equation*}`
`Range:(-\infty,\infty),\lbrace y:y\in\Re\rbrace`