Question

If a seed is planted, it has a 90% chance of growing into a healthy plant. If 9 seeds are planted, what is the probability that exactly 4 don't grow?

Answer 1

The Binomial Distribution

It's a discrete probability distribution commonly used to calculate the probability of repeated similar events, each with a success rate of p.

Suppose n trials are performed and we are interested in calculating the probability of occurrence of k successes.

The formula used is:

`P(k,n)=\binom{n}{k}p^kq^(n-k)`

Where q = 1 - p

The chance for a seed to grow into a plant is p = 0.90. This means q = 1 - 0.90 = 0.10.

If n = 9 seeds are planted, it's required to calculate the probability that exactly 4 don't grow. If 4 seeds don't grow, then k = 5 will grow.

Applying the formula:

`P(5,9)=\binom{9}{5}0.90^50.10^(9-5)`

Calculate the combinatorial number:

`\binom{9}{5}=\frac{9!}{5!\text{ }4!}=(9\cdot8\cdot7\cdot6\cdot5!)/(5!\cdot4\cdot3\cdot2\cdot1)=(3024)/(24)=126`

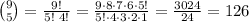
Now calculate:

`P(5,9)=126\cdot0.59049\cdot0.0001`

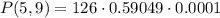
Finally:

P(5, 9) = 0.00744