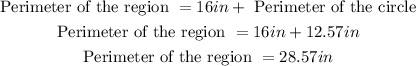Question

Find the perimeter of the region. 90° 90° 2 in.t + 6 in. . 90° 12 6 in. .

Answer 1

The perimeter is the sum of all the sides of a geometric figure. To find the perimeter of this figure you can add the straight sides and then add the perimeter of a circle with a radius equal to 2.

Then, you have

`\begin{gathered} \text{ Perimeter of the region }=2in+6in+2in+6in+\text{ Perimeter of the circle} \\ \text{ Perimeter of the region }=16in+\text{ Perimeter of the circle} \end{gathered}`

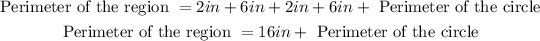
The formula to find the perimeter of a circle is

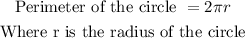
`\begin{gathered} \text{Perimeter of the circle }=2\pi r \\ \text{Where r is the radius of the circle} \end{gathered}`

So,

`\begin{gathered} \text{Perimeter of the circle }=2\pi r \\ \text{Perimeter of the circle }=2\pi\cdot2in \\ \text{Perimeter of the circle }=12.57in \end{gathered}`

Finally, the perimeter of the region will be 28.57 inches.

`\begin{gathered} \text{ Perimeter of the region }=16in+\text{ Perimeter of the circle} \\ \text{ Perimeter of the region }=16in+12.57in \\ \text{ Perimeter of the region }=28.57in \end{gathered}`