we know that
Use the value of the discriminant to determine the nature of the solutions to the quadratic equation.
so
The discriminant is equal to
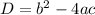
Part 23
we have
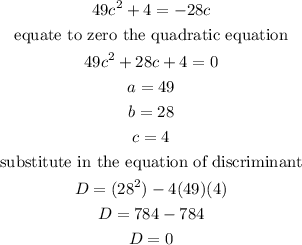
that means -----> the roots are equal and real.
part 24
we have

that means -----> The discriminant is negative, so the equation has two non-real solutions.
Part 26
we have
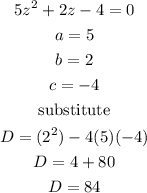
that means -----> The discriminant is positive, so the equation has two distinct real solutions.