In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
table
Step 02:
data table:
graph:
point 1 (15 , 19)
point 2 (20, 26)
slope = m:
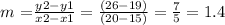
slope = m = 1.4
point-slope form of the line:
(y - y1) = m (x - x1)
(y - 19) = 1.4 (x - 15)
y - 19 = 1.4x - 21
y = 1.4x - 21 + 19
y = 1.4x - 2
equation of the line:
y = 1.4x - 2
slope :
is the variation of the price depending on the weight
y-intercept:
x = 0;
y = 1.4x - 2
y = 1.4(0) - 2
y = - 2
y-intercept = - 2
y-intercept:
when the weight is equal to zero the price is $ -2
it would be more logical for the price to be zero when the weight is zero
That is the full solution