Before we start to answer we will calculate the final velocity of the car when it reaches the edge of the cliff which will be the initial velocity when the car starts falling. To do this we notice that while the car rolls down it has a constant acceleration which means that it is an uniformly accelerated motion and then we can use the equations:
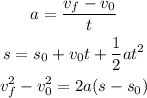
While the call rolls we know that:
The initial velocity is zero.
The change in position is 40 m.
The acceleration is 3.37 m/s².
Since we want to determine the velocity we use the third equation, then we have:
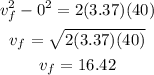
Hence, the car rolls down the cliff with a velocity of 16.42 m/s
a)
Once the car starts falling it moves in two directions, horizontally and vertically. Horizontally, since we have no force acting on the car, we have no acceleration and hence we have a rectilinar motion which can be described as:
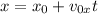
Since the cliff is inclined with an angle of 21° below the horizontal the initial velocity in this direction is:

To determine the time of flight we need to remember that, vertically, the car is following a an uniformly accelerated motion which means we can use the equation stated at the beginning of the solution.
Vertically, the initial velocity is:
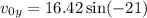
We also know that the car will move -30 m, and that the acceleration is -9.8 m/s²; since we want to determine the time we can use the second equation from the first set, then:
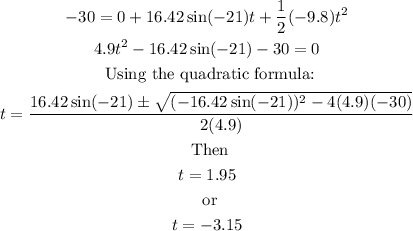
Since the time has to be positive we choose the positive solution; hence we conclude that the time the car is in the air is 1.95 s.
Now, that we know this we can find the distance the car is from the base of the cliff:
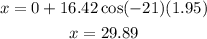
Therefore, the car is 29.89 m away from the base of the cliff.
b)
From the discussion of the time on part a we know that the car is in the air for 1.95 s