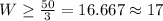since each ounce of whole mi contains twice as many calories as an ounce of skim milk, we have that W=2S where W repreents the number of calories in an ounce of whole milk and S represents the number of calories in an ounce of skim milk.
we can write the statement in the following inequality}
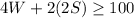
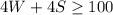
Then
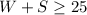
and since W=2S
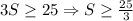
And
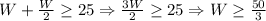
The final inequaities are:
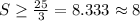
and