SOLUTION
Step 1 :
In this question, we are given the function f.
If the domain is restricted to {1,0),
We can see clearly that:
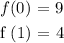
which makes it a one-to-one function.
Step 2 :
A function f is one - to -one if no two elements in the domain of f correspond to the same element in the range of f.
In other words, each x in the domain has exactly one image in the range.
And, no y in the range is the image of more than one x in the domain.
Step 3 :
In fact, only one-to-one functions have an inverse.
If a function is many-to-one the process to reverse it would require many outputs from one input contradicting the definition of a function.
CONCLUSION:
The inverse of f exists.