Question

1. Find the center of the circle that can be circumscribed about AABC.8942B26C8

Answer 1

Given:

The coordinate of the points A(0,0), B(0,4) and C(6,4).

Required:

Find the center of the circle that can be circumscribed by triangle ABC.

Step-by-step explanation:

We know that the center of the circle lies at the point of intersection of the perpendicular bisector of the three sides of the triangle.

The sides that join the point (0,4) and (6,4)that is perpendicular bisector is

`\begin{gathered} x=(0+6)/(2) \\ x=3 \end{gathered}`

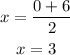
The mid point of the side joins the point (0,0) and (6,4) is

`\begin{gathered} mid-point\text{ = \lparen}(0+6)/(2),(0+4)/(2)) \\ =(3,2) \end{gathered}`

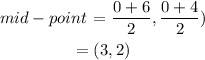
The slope of the line that joins the points (0,0) and (6,4) is

`\begin{gathered} Slope\text{ = }(4-0)/(6-0) \\ =(4)/(6) \\ =(2)/(3) \end{gathered}`

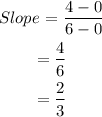
Now the slope of the perpendicular line is

`-(2)/(3)`

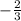
the equation of the perpendicular line is:

`\begin{gathered} y+x=3-2 \\ y+x=1 \end{gathered}`

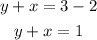
Le t the center is (a,b) that lies on both lines