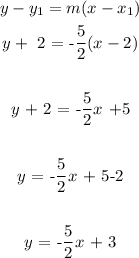Answer:
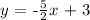
Step-by-step explanation:
The general equation of a straight line is:
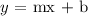
where m is the slope and b is the y-intercept
For the line given, the slope value is 2/5
When two lines are perpendicular, the product of their slopes is -1
Thus, from the slope of the first line, we can get the slope of the second line
Let us call the slope of the second line m2
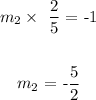
We have the slope of the second line and a point (2,-2) through which the line passes
We can write the equation of the line using the point-slope form as follows: