First, we need to find the interest. This is given by
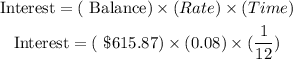
which gives

a) What is the amount of the final payment?
The final payment is given by
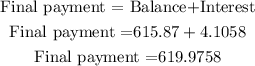
Then, the answer is $619.9758
b) How much does he save by paying the loan off early?
Since the loan is for 12 months, the total payment is
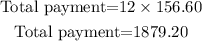
Therefore, the amount saved is given by
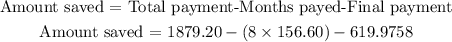
which gives
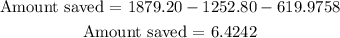
Therefore, the answer is $6.4242 saved