The question gives us the following information:
Principal = $8,000
Time = 1 year
Interest rate = 4.25%, compounded quarterly.
We're going to use the following formula to solve the questions:
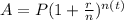
Where A is the total amount at the end of the investment, r is the annual interest rate, n is the number of compounding periods in a year, and t is the time in number of years.
By substituting the given, we get:

Therefore, the amount is $8,345.46.
Interest earned is the additional money received from the investment. So we simply subtract the principal from the total amount.
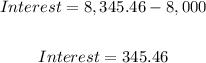
So interest is $345.46.
Lastly, to find the annual percentage yield, we divide the interest earned by the principal amount invested.
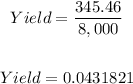
The yield is 0.043182 or 4.318%.