Question

A company makes steel rods shaped like cylinders. Each rod has a radius of 3 centimeters and a height of 40 centimeters. How much steel willthe company need to make 121 rods?Use 3.14 for “pie” , and do not round your answer.

Answer 1

136778.4 cm³

Step-by-step explanation

First we have to find how much steel is needed to make one rod. We know that they are shaped like cylinders, so we use the volume of a cylinder formula:

`\begin{gathered} V=B\cdot h \\ V=\pi\cdot r^2\cdot h \end{gathered}`

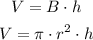
In this case r = 3cm and h = 40cm. We have to use pi = 3.14:

This is the volume of one rod. Now, to find how much steel the company needs for 121 rods, we just have to find the volume of 121 rods - i.e. multiply the volume of one rod by 121:

The company needs a volume of 136778.4 cm³ to make 121 rods with the given dimensions.