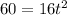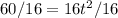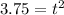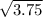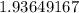Question

Due to gravity, an object falls 16t^2 feet in t seconds. You drop a backpack from a window that is 60 feet above the ground. Will the backpack hit the ground in 2 seconds?

Please try and explain the question as well!

Answer 1

yes, the backpack will hit the ground in ~2 seconds (
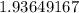`1.93649167` seconds)

Step-by-step explanation:

to find out, we use
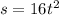`s=16t^2`, where
`s` = distance from ground and
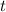`t` = time

as we are given 60ft for the distance from the ground, the equation turns into
`60 = 16t^2`

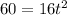
to find
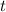`t`, divided both sides by 16 to get
`3.75 = t^2`

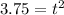
then get the square root of
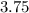`3.75`, which is
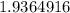
`1.9364916`

-----------------

`60 = 16t^2`

`60/16 = 16t^2/16`

`3.75 = t^2`

`√(3.75)`

`1.93649167`