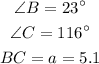Given:
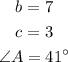
To find: The missing sides and angles
Explantion:
The formula of cosine,
![a=\sqrt[]{b^2+c^2-2bc\cos A}](https://img.qammunity.org/2023/formulas/mathematics/college/7xnbkep3x12652wrj0g8xjrt1mq7q2ig18.png)
Substituting the given values we get,
![\begin{gathered} a=\sqrt[]{3^2+7^2-2(3)(7)\cos 41^(\circ)} \\ =\sqrt[]{9+49-42\cos41^(\circ)} \\ =\sqrt[]{26.3021} \\ =5.12857 \\ \approx5.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fg6jody63dpev29dlhq5t0exsjfi94kgvc.png)
Thus, the missing side length is a = 5.1.
Using the sine formula,
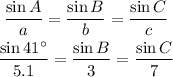
Solving first two terms we get,
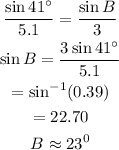
Thus, the measure of angle B is 23 degrees.
Using the angle sum property,
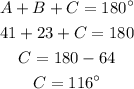
Thus, the measure of angle C is 116 degrees.
Final answer: The missing angles and sides are,